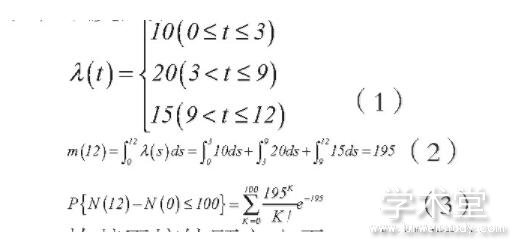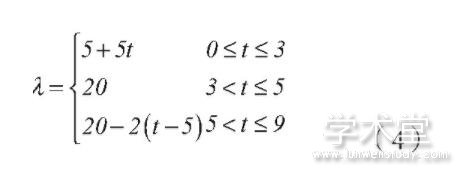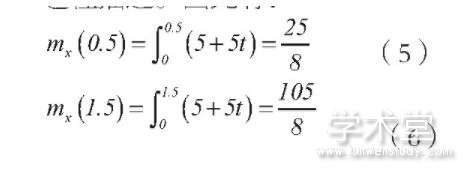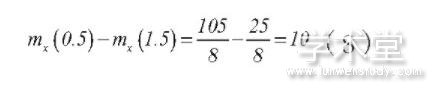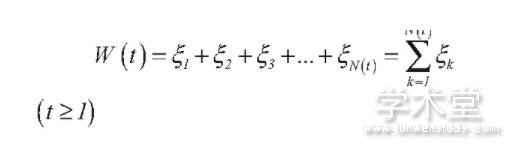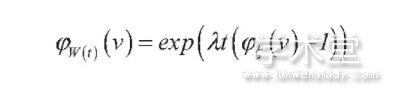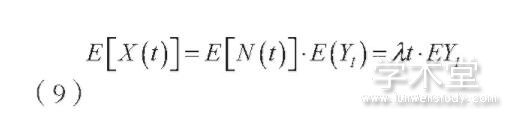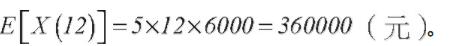数学与生活论文第四篇:泊松过程在商场管理和寿险问题中的运用
摘要:泊松过程是一种累计随机事件发生次数的最基本的独立增量过程。泊松过程可以用来描述许多偶然现象。着名的例子包括盖木多计数器上的粒子流,细胞中染色体的交换次数,电话交换台所接到的呼叫次数,交通流中的事故数,编码中的误码流,股票市场中买进或卖出股票的次数等等。泊松过程不光在工业和商业中有所涉及,在经济和金融方面都有着极其重要的作用。本文结合一些实例给出了泊松过程在经济生活领域里的一些简单应用。阐述了其在经济生活中的重要作用和应用价值。
关键词:泊松过程; 经济生活; 人寿保险;
discussion on the application of poisson process in economic life
Wang kangkang
一、序言
泊松过程是经济生活中非常重要的分布形式。例如,在公交车站固定时间内到达的乘客数量也近似地服从泊松过程。此外,泊松过程也存在于大量服务系统中,因此泊松分布在运筹学和管理科学中起着重要作用。如物料订单的规划,道路交通信号灯的设计,生产计划的安排,出货时间表的安排等等都需要用到泊松过程。同时,在物理学中,热电子的发射、显微镜下落在某区域中的血球或微生物的数目等也都近似于泊松过程。在工业生产中,每米布的疵点数、纺织机上每小时的断头数、每件钢铁铸件的缺陷数等也近似地服从泊松过程。
另外,天空中一定时间内流星的数量,溶液中微生物的浓度等都服从泊松过程。因此,可以看出泊松过程是具有广泛应用范围的基本且重要的过程。下面将主要举出在国民经济中的一些泊松过程的例子。
二、泊松过程在商场管理中的应用
例1:商店每天营业12个小时,前三个小时到达的顾客平均为10人/小时,
最后三个小时到达的顾客平均为15人/小时,中间6个小时到达的顾客20人/小时.求某天接待顾客少于100人的概率。
解:设顾客流N(t)为非齐次泊松过程,强度函数
故某天接待顾客少于100人的概率为。
例2:某商店每天八点开始营业,从八点到十一点平均顾客到达率成线性增长,顾客平均到达率在八点的时候为每小时5人,顾客到达率在十一点的时候最大为每小时20人。从十一点至下午一点,平均顾客到达率保持不变,是每小时20人,从下午一点至五点,顾客到达率线性下降,到下午五点顾客到达率变成每小时12人。如果到达商店的顾客数在不相重叠的时间区间内是相互独立的,那么在八点半到九点半之间没有顾客到达商店的概率为多少,在这一时间区间内顾客到达商店的数学期望为多少?
解:将时间从八点至下午五点平移为零点到九点,那么得顾客到达率为:
由题意,顾客的变化可用非齐次泊松过程描述。因此有:
在十二点半到一点半没有顾客到达商店的概率:
即在八点半到九点半没有顾客到达商店的概率为e-[10]。
所以顾客在这一时间区间内到达商店的数量的数学期望:
三、泊松过程在人寿保险问题中的应用
设N(t)表示在时间区间(0,t]内持有保险单且已死亡的人数,由于更新计数过程{N(t),t≥0}服从参数为λ的负指数分布,故随机过程{N(t),t≥0}为齐次泊松过程。同时,若保险公司在时间间隔(0,t]内,对所有持有保险单且已死亡人员支付的总金额为W(t),而第k个持有保险单人员,在τk时刻死亡时,向保险公司索赔的所有保险金为ξk,显然{ξk,k=1,2,3...}是随机序列,且有以下关系式成立:
又ξ1,ξ2,ξ3,...,ξN(t)相互独立,但无论哪一个持有保险单人员死亡时,向保险公司索赔的所有保险金额分别为ξ1,ξ2,ξ3,...,ξN(t)等,都需要服从相同的概率密度分布函数fξ(s)(其中s为持有保险单人员终生领取保险金的时间间隔)。总之,随机序列ξ1,ξ2,ξ3,...,ξN(t)是独立且同分布的。又因为保险公司支付给某死亡人员的保险金ξk,与当时所对应的第N(t)个死亡者无关,所以我们可以认为{ξk,k=1,2,3...}与{N(t),t≥0}也是相互独立的。
综上所述,人寿保险过程
{W(t),t≥0}属于复合泊松过程的范畴。
可由上面的结论,计算出W(t)的数字特征。
1、W(t)的特征函数
说明保险公司支付的总金额W(t)的特征函数与每一个持有保险单人员死亡时所索取的所有保险金金额ξ的特征函数有关。
2、W(t)的数学期望E{W(t)}=λtE(ξ)
说明{W(t),t≥0}是非稳恒过程,其均值E{W(t)}随时间t而随机变化,有一定的风险性。E{W(t)}与tE(ξ)成正比,比例常数为泊松流强度λ。
(3)W(t)的方差V ar{W(t)}=λtE(ξ[2])
说明Var{W(t)}与t E(ξ[2])成正比,比例常数为泊松流强度λ。Var{W(t)}显示了随机变量W(t)在人寿保险过程中的一切可能之值在其均值E{W(t)}周围的分散程度,E(ξ[2])越大,t越长,则W(t)也越分散,Var{W(t)}之值越小越好,否则在(0,t]这一漫长的时间间隔内,保险公司所赔付的保险金总金额W(t),变化起伏较大,不便对其进行宏观调控,所以我们一般把所历时间取成三年或五年为一次单位进行结算。而ξ概率密度分布函数fξ(s)可用负指数分布模拟。
复合泊松过程还具有泊松分布的可加性。在经典风险模型中的一些较好的结论,如破产概率的渐进性、上界、破产瞬间盈余分布等由于索赔过程的复杂性很难在新的模型中得到类似证明。这样可以把两个泊松过程描述的索赔过程化简为一个复合泊松过程描述的索赔过程。
故对于复合泊松过程来说,在λ较大时,我们可以用正态过程近似,同时也就可以运用正态过程的一些特性,从而更好的解决问题。
例3:设保险公司接到的索赔次数服从强度为λ=5次/月的泊松过程,每次理赔数均服从[2000,10000](单位:元)上的均匀分布,则一年中保险公司平均赔付总额是多少?
解:由题意,保险公司一年的赔付总额,其中{N(t),t≥0}为参数λ=5的泊松过程,{iY,i=1,2,...}为相互独立的[2000,10000](单位:元)上的均匀分布随机序列。由复合泊松过程的定理
故一年平均理赔总额为
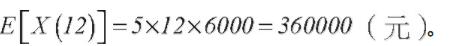
参考文献
[1] 杜雪樵,惠军.随机过程[M].合肥工业大学出版社,2009.
[2]刘次华.随机过程[M].华中科技大学大学出版社,第五版,2014.
[3]王丽燕,沈玉波,刘洪.随机过程[M].大连理工大学出版社,2008.
[4]何选森.随机过程[M].人民邮电出版社,2009.
[5]方开泰,许建伦.统计分布[M].高等教育出版社,2016.
[6] 茆诗松,程依明,濮晓龙.概率论与数理统计[M].第二版,2015.
[7] 刘玉琏,傅沛仁.数学分析讲义(下册)[M].北京:高等教育出版社,1986.
[8]欧阳光中等.数学分析[M].上海:上海科学技术出版社,1982.
[9]陈凤腾,左洪福,王华伟,倪现存,白芳.基于非齐次泊松过程的航空备件需求研究和应用[J].系统工程与电子技术.2007(09).
[10]王东升,刘玉堂.泊松过程在排队论中的应用[J].河南机电高等专科学校学报.2007(04).
点击查看>>数学与生活论文(精选论文8篇)其他文章