摘 要: 针对事件树中的环节事件概率存在的诸多不确定性和模糊性,提出了基于模糊数学理论的溃坝概率计算分析方法,通过将事件树与模糊数学理论相结合,采用模糊数参照专家评判意见进行量化处理,从中求解大坝溃决环节事件中的概率值,为水库大坝溃决风险计算提供了新的思路。
关键词 : 事件树;大坝;溃决;模糊数;环节概率;
Abstract: In view of the many uncertainties and ambiguities in the event probability of the links in the event tree, a calculation and analysis method of dam break probability based on fuzzy mathematics theory is proposed. By combining event tree with fuzzy mathematics theory, use fuzzy numbers to refer to expert opinions for quantitative processing, solve the probability value in the event of the dam failure link from it, provides a new idea for calculating the risk of dam failure of the reservoir.
Keyword: event tree; the dam; dam break; fuzzy number; link probability;
1、 概述
水库溃坝作为一种偶然事件,发生的概率比较小,但造成的损失却不可估量,对下游人员财产造成巨大的破坏,大坝的安全问题受到了更加广泛的关注和重视,因此,研究大坝溃决的风险及其失事发生的可能性成为了摆在水利工作者面前的一项重要议题。
大坝溃决概率作为大坝风险分析的重要组成部分,国内外学者也进行了深入的研究,并取得了一些成果。
就国外而言,国外学者Steven G.Vick和 J.Barneich于1999年总结提炼出来溃坝风险概率经验估算表,在此基础上进行了深入研究,取得了一系列成果[1];就国内而言,诸如南京水利科学研究院李雷、王仁钟等[2]在分析总结我国大坝现状特点,参照国外现有研究成果的基础上,对大坝风险概率经验估算表进行了更为深入的探讨研究,使其更加细化、更加实用,但在针对大坝风险分析环节概率取值更具针对性的同时,也难免存在一定的人为因素,且需要借助大量历史资料才能做出估值,缺乏足够的理论支撑。
总体来看,大部分研究成果可概括为:历史资料统计法与可靠度法及专家经验法,主要依赖于专家经验估算及定性描述,但前提是,需要借助大量水库溃坝失事统计数据资料的基础上做出分析评判,由于我国在水库溃坝资料统计收集方面较为欠缺,相比国外还有很大差距,统计资料的匮乏无疑给大坝风险分析研究带来了一定的困难。尤其是溃坝概率计算的“环节概率”大多采用事先制定的经验表格进行一定范围内的取值,存在主观人为性,难以做到公正、客观地评价大坝发生可能性的大小,其计算出的大坝溃坝概率值得进一步商榷。
因此,本文在参考分析现有研究方法及成果的基础上,结合模糊数学,引入“模糊数”对大坝失事的环节概率进行计算,同时采用事件树理论构建大坝溃决概率分析树状图。一方面使其有理论依据可寻,更具科学性,另一方面,可提高溃坝概率计算成果的准确性和可信度。

2、 事件树法
2.1、 事件树分析原理
事件树分析法(ETA)是复杂系统或体系中基于安全检测及隐患排查为目的的一种逻辑推理分析方法,它可以从事故的结果中推断寻找发生的原因,该方法已普遍应用到诸多学科领域,基于此,此方法可用于大坝溃坝失事全过程预测分析,通过环节失事概率计算,最终推求大坝溃决风险。
2.2、 大坝溃决事件树的构建
1)原理及步骤。
采用事件树分析时,主要考虑在库水位的作用下,推求大坝失事后果的风险,通过对坝体不同部位失事可能性进行分析,构建溃决失事事件树状图,列出不同的失事路径,对不同路径上引起事件的因子进行概率计算,给出环节概率值,在此基础上,计算每条路径上发生溃决的概率,对所有不同路径上发生溃决的概率进行相加,由此得到该水位荷载作用下的大坝溃决概率,见图1。
图1 事件树溃坝概率计算步骤

2)环节事件发生概率的求解。
事件树结构如图2所示,事件树分析示意图如图3所示。
图2 事件树结构
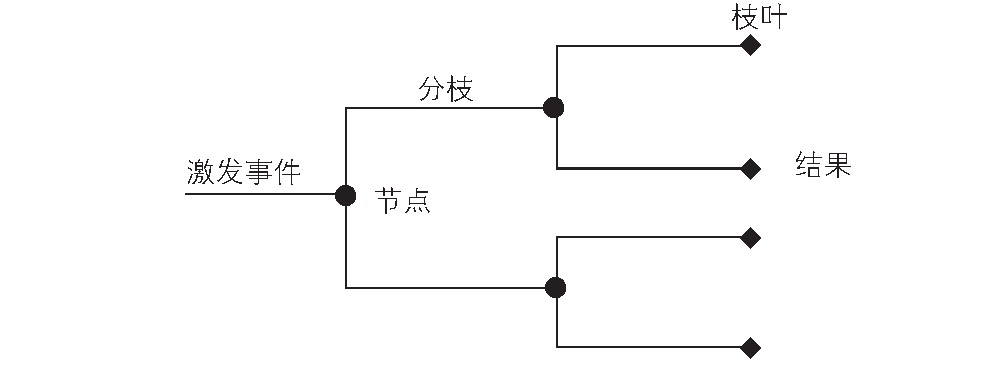
大坝失事激发事件,通常以水荷载(地震、人为因素等)为代表,导致大坝出现失事风险,经过一系列“环节”,最终引起溃坝,因此,需对“环节概率”采用相关理论方法进行分析评判,结合专家意见,得出相关计算结果。同时采用“模糊数”进行数量化,为尽量避免人为主观性,需要对同一环节概率值进行算术平均值计算,最终确定该环节发生的概率值。
图3 事件树分析示意图
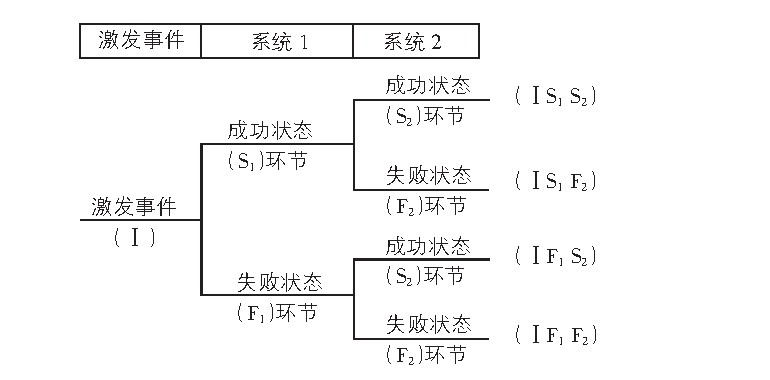
P???i=xi1+xi2+?+xinn=∑i,j=1nxijn (4)
其中,P???i为大坝失事的过程中某环节的溃坝概率;xij为j专家对溃坝i环节的评判结论;n为专家数量或大坝溃坝环节数量(i,j=1,…,n)。
3、 模糊数与隶属函数
3.1、 三角模糊数与隶属函数
针对域内X中的某一模糊集A*,假设?x∈A*存在某一元素μA*(x)∈[0,1]与其相呼应,则将μA*(x)视作x对A*的隶属度,此时,μA*视为A*的隶属函数[3]。
模糊数可针对溃坝环节概率中专家的定性描述语句转化为定量的概率计算,常见的有三角模糊数和梯形模糊数,其中,三角模糊数集用A*=(a,b,c)来描述(见图4),隶属函数为:
3.2、 梯形模糊数及其隶属函数
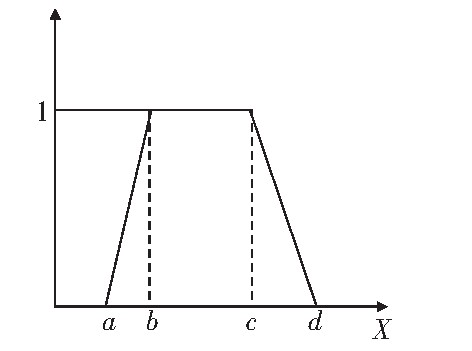
梯形模糊数集采用A*=(a,b,c,d)来描述(见图5),隶属函数如下:
3.3、 模糊数计算
当0≤λ≤1,λ截集可按下式计算:
其中,Aλ与Bλ在实数轴上的非空边界区间分别为Aλ=[AλL,AλU],Bλ=[BλL,BλU],AλL,AλU,BλL,BλU分别为区间上的上、下界,则三角模糊数A=(a,b,c)和梯形B=(a,b,c,d)用λ—截集如下所示:
图4 三角隶属函数
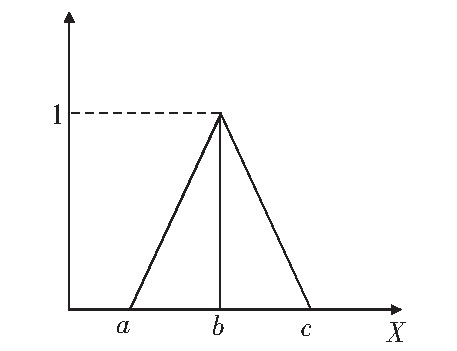
图5 梯形隶属函数
模糊数的λ—截集运算法则[4]:
3.4 、模糊数的非模糊化
1)专家判断语言的转化。
针对专家给予溃坝环节最初的定性判别,需要对专家的判别结论进行定量表达,此时即为专家模糊判别语言[5]的非模糊化处理,可参照表1。专家评判模糊性语言的隶属函数见图6。
表1 定性评判语句与模糊数的转化计算表
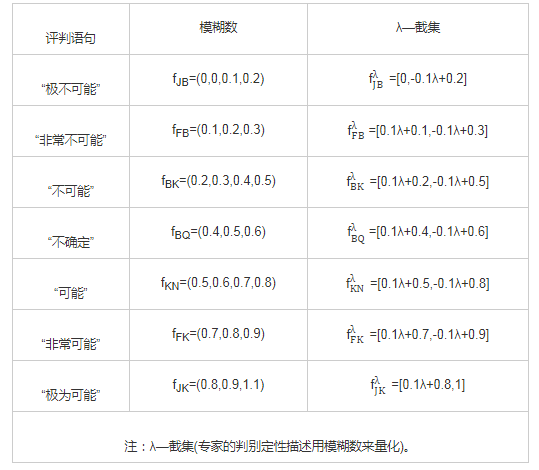
注:λ—截集(专家的判别定性描述用模糊数来量化)。
图6 专家评判模糊性语言的隶属函数
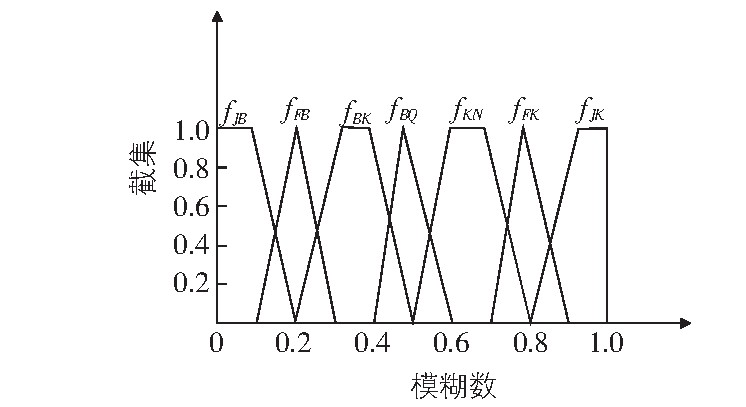
2)模糊数的求解。
模糊数的求解目的在于把专家对溃坝发生的某一环节做出的评判语言定性描述进行直接定量的数值化处理,该过程称之为模糊数的量化。模糊数的量化方法,通常有Chen[6]提出的“max”或“min”集合的方法;Kim等[7]提出的乐观系数法,上述方法各有特点,Liou[8]提出的积分值法综合了上述两种方法的优点。因此,本文采用Liou积分值法,综合考虑λ—截集与模糊数的关系,针对LR类型的模糊数,求其隶属函数的反函数的积分值。
Iα=αIR(A*)+(1-α)IL(A*) (10)
其中,IL(A*),IR(A*)分别为模糊数左、右隶属函数的反函数的积分值;α为乐观系数,α∈[0,1]。IL(A*)及IR(A*)可借助λ—截集进行求解:
其中,λu(A*)和λl(A*)分别为模糊数A*的λ—截集的上、下界,λ=0,0.1,0.2,…,1;Δλ=0.1,当α=0及α=1时,代表模糊数A*上、下界。
4 、工程实例
江西赣州某水库为一座具有综合利用的大(2)型水库,5000 a一遇洪水校核,100 a一遇洪水设计,水库校核洪水位224.75 m, 正常蓄水位220.0 m, 死水位209.0 m, 总库容为1.19亿m3,工程枢纽主要建筑物有:主、副坝,溢洪道,发电引水隧洞等。
采用本文提出的理论方法进行溃坝风险率估算,在构建溃坝风险事件树的基础上,针对溃坝环节概率采用模糊数,通过定性语言的描述转化为定量计算数值,同时依据专家意见及建议成果的选取,以主坝坝基管涌溃坝风险事件树(库水荷载223.70 m)为例进行溃坝概率计算分析(见图7,表2,表3)。
图7 主坝坝基管涌溃坝风险事件树(汛期水位荷载223.70 m)
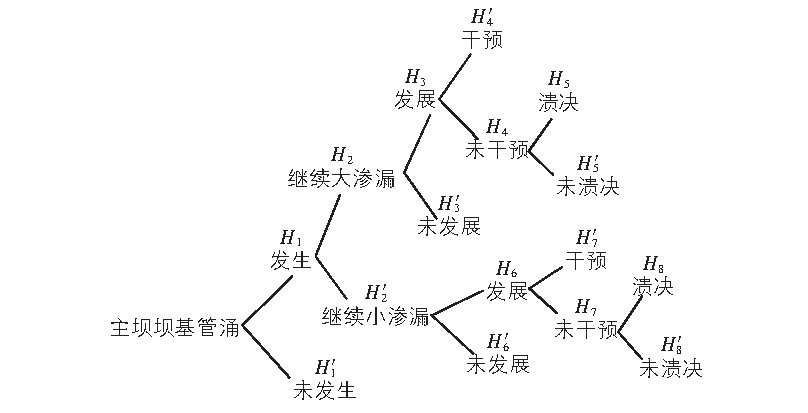
表2 汛期洪水(223.70 m)荷载下,主坝坝基发生管涌的概率估算
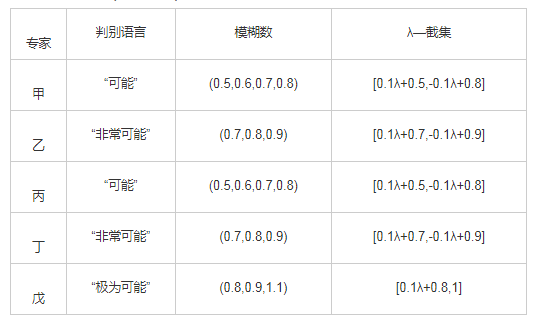
表3 校核水位(223.70 m)工况下,主坝坝基管涌溃坝相关环节概率
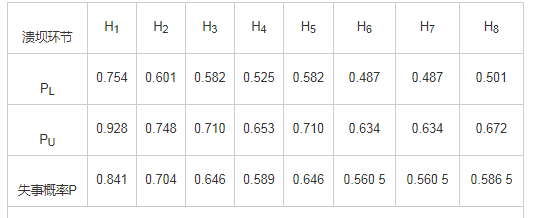
注:H1,H2,…,H10均为环节概率;PU,PL分别为失事环节概率模糊数的上、下界。
经过计算,可得到汛期洪水(223.70 m)荷载下,主坝坝基管涌溃坝概率为3.83×10-5,占总溃坝概率的11.52%。因此,水库汛期,建议重点加强主坝坝基部位的巡查和检查。
5 、结语
本文在总结分析现有大坝溃决概率研究成果的基础上,指出了现有溃坝概率计算方法存在的不足。针对溃坝环节概率计算,提出了采用模糊数学理论结合事件树法的大坝溃决概率计算方法及步骤,并结合工程实例进行了分析计算。主要有以下几点体会:
1)本文所提出的模糊数学理论结合事件树的大坝溃决概率计算方法,是集模糊数学理论、专家经验、智慧为一体,并结合工程实际运行情况及参照相关资料的基础上做出的科学评判,基于此,溃坝环节概率的计算更具理论性和可行性,在一定程度上避免或降低了盲目套用国外经验表格对溃坝环节概率做出估值的主观人为性。
2)模糊数学理论结合事件树的大坝溃决概率计算方法中的环节概率计算工作量较大,其专家模糊语言的非模糊定量化求解方法,有待进一步研究,环节概率的计算,有必要通过进一步研究,采用计算机程序进行自动识别计算,以此减少工作量,提高工作效率。
参考文献
[1] Steven G.Vick. Degrees of Belief: Subjective Probability and Engineering Judgement[M] America:ASCE press, 2002.
[2]李雷,王仁钟,盛金保,等大坝风险评价与风险管理[M].北京:中国水利水电出版社, 2006.
[3]杨纶标,英仪模糊数学原理及应用[M].广州:华南理工大学出版社, 1993.
[4]李洪兴,汪群,段钦治,等.工程模糊数学方法及应用[M].天津:天津科学技术出版社, 1993.
[5] Lin Ching-torng,Wang Mao-Jiun J.Hybrid fault tree analysis using fuzzy sets[J]. Reliability Engsyst Safety,1997 58(3):205-213.
[6] Chen S H.Ranking fuzzy num bers with max imizingset and minimizing set[J].Fuzzy Sets and Syst, 1985, 17(2)-113-129.
[7] Kim K,Park K s. Ranking fuzzy numbers withindex ofoptmism[J] Fuzzy Sets and Syst,1990,35(2):143-150.
[8] Liou Tian-shy,Wang Mao-jiun J.Ranking fuzzy numbers with in tegralva lue[J]Fuzzy Sets and Syst,1992 ,50(3).247-255.





