第4章 数学史融入高中数学的概念教学的案例分析
从前面的研究及实际情况来看,将数学史附加于数学教学的做法并不能被多数学生认可。 如果数学史给学生带来的只是兴趣,那么他们宁可花这些时间多做几道题目。 并且在应用数学史的层次上,只是停留在激发兴趣的层面显然是不够的。所以,如何提高应用数学史的层次,使得数学史材料能让学生对数学概念的理解有所帮助,是目前需要解决的焦点问题。 也就是说需要挖掘数学史的深层次的作用,使得数学史真正融入高中数学的概念教学之中。而对于教师而言,也需尽可能的简单易行可操作。为此,笔者尝试对高中数学概念教学中几个常见难点进行了数学史融入的相关教学设计,希望能形成一个教学模式。
4.1 数学史融入函数中的概念教学的案例设计
《普通高中数学课程标准》指出数学课堂教学应“努力揭示数学概念、结论发展过程,体会蕴涵在其中的数学方法,追寻数学发展的历史足迹,把数学的学术形态转化成学生容易接受的教育形态。”章建跃先生提出,教师必须十分重视数学概念教学,尤其是数学核心概念的教学。 怎样合理、有效地设计、组织教学,有利于学生更好地理解数学概念?这是值得每一位教师思考和研究的课题。 事实上,数学概念并非凭空而来。 我们所学的数学概念,大都有着各自产生的背景和发展演变的过程,其间凝聚了数学家们的心血和智慧。“对数”是函数这一章节中的核心概念之一,对数概念的学习一直是高中学生学习数学的一大障碍。 很多学生直到高考都没有真正理解对数的概念,一看见对数就犯怵。
M.克莱因认为,历史上许多大数学家所遇到的困难,也正是学生也会遇到的学习障碍,因此历史是教学的指南。 他认为:“课本中的字斟句酌的叙述,未能表现出创造过程中的斗争、挫折,以及在建立一个可观的结构之前,数学家所经历的艰苦漫长的道路。 而学生一旦认识到这些,他将不仅获得真知灼见,还将获得顽强地追究他所攻问题的勇气,并且不会因为他自己的工作并非完美无缺而感到颓丧。”因此,笔者尝试运用数学史的有效融入方式,结合学情,对教材进行“二次开发”,采用重构式教学方法,促进学生理解对数概念。
4.1.1 创设情境,引出新知

4.1.2 以史为鉴,追根索源
师:我们首先来看看数学家们是如何来解决这个问题的。
对数的基本思想可以追溯到遥远的古希腊时代,那个时候,阿基米德(Archimedes,公元前 287~ 公元前 212 年)就已经研究过几个 10 的连乘积和 10 的个数之间的关系,用现代的表达形式来看,就是研究了这样两个数列:
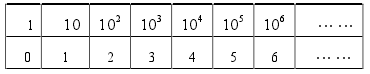
他发现它们之间有某种对应关系,但是阿基米德虽然发现了规律,却没有把这项工作继续下去,失去了对数破土而出的机会。
15、16 世纪的欧洲,航海和贸易的迅速发展,极大地推动了天文学和三角学的进步。 特别是地理探险需要更为准确的天文知识,为了确定行星的位置或制作天文数表,往往要花上几天甚至几个月的时间进行计算。对计算速度和准确性的要求与日俱增,人们希望将乘、除、乘方、开方归纳为简单的加、减、乘、除来实现。
15 世纪,法国数学家许凯(N.Chuquet, 1445~ 1488)在两个数列中也发现了类似的对应规律。他在其着作《算学三部》中给出了双数列

之间的对应关系:上一列数之间的乘、除运算结果对应于下一列数之间的加、减运算结果,如4 ? 32 = 128,对应于2 + 5 = 7.16世纪,德国数学家斯蒂菲尔(M.Stifel,1487~ 1567)针对双数列更明确地提出了上一列数的乘、除、乘方和开方四种运算法则。 还有其他很多数学家也发现了这样的规律,但是由于种种原因,特别是分数指数还没有得到认识,所以他们也没有发明对数。
那同学们,我们刚刚学习了分数指数幂,比这些古时候的大数学家们掌握了更丰富的数学知识,我们是不是一起来发明对数呢?
请学生先观察刚才的两组数,到底阿基米德、斯蒂菲尔等数学家发现了怎样的规律呢?
组织学生进行分组讨论,教师适当引导,要求结合指数运算法则。
得出结论:下面一列数的加减运算结果与上面一列数的乘除运算结果有一种对应关系。
师:能否用一个指数的运算法则来表述这个关系?
生:同底数幂相乘,底数不变,指数相加。
师:很好,看来同学们对前面的内容掌握的不错。
那么,时间的长河流至 16 世纪至 17 世纪初,这个时期,各个领域的科学知识都在急速地发展。 但是,这些科学知识发展也带来了庞大的数学计算需求。 特别是天文学、航海学、商业贸易、工程和军事,它们对于计算速度和准确率的要求与日俱增。 这个时期,哥白尼的“太阳中心说”开始流行,导致天文学成为当时最热门的学科之一,以精确测量为基础的天文学的随之兴起,天文学家们不得不去计算那些繁杂的“天文数字”,这些超复杂的计算耗费了他们大量的精力,有的天文学家甚至浪费了毕生的宝贵时间。 比如,为确定一颗星球的位置,天文学家常常在计算上花去好几个月的时间。 面对这样惊人的数字,这么笨拙的计算方法,怎样才能简化运算,能不能用加减运算来代替原来的乘法运算,就成了当时人们,特别是数学家们迫切需要思考的问题。
我们能不能一起来解决这样一个问题呢?
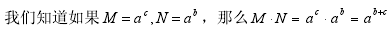
刚才第二组数据中,第一行表示 2 的对应幂,第二行表示 2 的指数,那么,如果我们要计算第一行中两个数的乘积,就可以通过第二行中对应数字的加和减来实现。 比如,计算 16? 64的值,就可以先查询第二行的对应数字:16对应4,64对应6 ,然后再把第二行中的对应数字加起来: 4 + 6=10,第二行中的10对应第一行中的1024,所以有: 16 ? 64=1024.
也就是说如果我们有类似这样一张表格,就可以通过指数的加减运算来得到幂的积或商。
那在具体实施的过程中,我们最好能把指数表示出来。也就是说如果 N 可以用ba 来表示,那么b 可以用N 表示吗?
教学意图:提供对数知识历史背景和原始问题,增强真实感,引发学生进行探究,追溯数学家发现对数的过程,通过观察分析表格中双数列对应关系,使学生深刻认识到对数对简化运算的重大作用和引进对数的必要性。 同时,通过丰富的情景和动人的数学家的历史故事,激发学生的求知欲和创造欲。
4.1.3 以史促思,建构概念
后来,英国数学家纳皮尔(J.Napier, 1550~ 1617)受到上述表格的启发,发现了可以利用这个规律来简便运算的有效工具,于1614年出版《奇妙的对数定理说明书》,这标志着对数的诞生。 为了这一划时代意义的发明,纳皮尔整整花费了二十多年时间!他把b 称为N 的“对数”,今天,我们依然沿用这个称呼,把b 称为以a为底N 的对数。 17世纪,笛卡儿(R.Descartes, 1596~ 1650)发明了幂的记号,指数概念才应运而生。直到17世纪末,才有人认识到对数可以定义为幂指数。
之后,欧拉(L.Euler, 1707~ 1783)深刻揭示了指数与对数之间的密切联系,并创

教学意图:引导学生在指数式与对数式之间进行互化的过程中,进一步认识对数概念的本质,加深对对数概念的理解,掌握其互化方法。从中让学生感受转化与化归思想方法,学会用联系的观点分析问题和处理问题。
4.1.4 以史为镜,深化理解
为了使纳皮尔发明的对数可以更方便地被人们使用,对数历史上的另一位重要人物英国数学家布里格斯(Briggs,Henry,1561~ 1630)和纳皮尔决定把 10 作为对数的底。 纳皮尔去世后,布里格斯又对纳皮尔的对数进行了改进,他把 10 进行了 54 次的开平方后,得到了一个略大于 1 的数,并取 10 作为对数的底,造出了常用对数表。 比如思考 2 中的(3),底数为 10,这样的以 10 为底的对数就称为常

4.1.5 以史启真,诱发再探
师:1971年的5月15日 ,尼加拉瓜发行了一套名为“改变世界面貌的十个数学公式”的数学纪念邮票 ,其中就有我们刚刚学习的纳皮尔指数与对数关系公式。
拉普拉斯曾经说过:“对数的发现,以其节省劳力而延长了天文学者的生命。”伽利略宣称:“给我时间 、空间和对数 ,我可以创造出一个宇宙来。”由此可见,对数在天文学和自然科学中有重要作用。恩格斯把对数的发明和解析几何的创造、微积分的建立称为17世纪数学的三大成就和“最重要的数学方法”.那今天的课堂上我们了解了那些知识呢?
生:我们了解了对数的诞生过程,学习了对数的概念,以及指数式、对数式之间的互化。
生:指数式、对数式之间的互化中体现了转化思想。
师:同学们畅所欲言的讨论,既梳理了指数、对数等相关知识的内容,又寻味了对数发展史的各个阶段所凝聚的思想、智慧与精神。按照研究数与函数的方法,接下来研究什么呢?
生:对数的运算规律(性质)和对数函数概念及其性质。
师:很好!今天我们认识了对数,感受到了数学家们思考问题的奇妙历程和智慧,也感受到了数学发展推动人类认识世界的巨大力量。希望大家课后通过练习,进一步巩固、理解和掌握对数的概念,明天我们将继续来研究对数的一些运算性质,进一步学习这个新的认识世界的工具!
教学意图:课堂小结意在画龙点睛,让学生对所学的知识作简单的回顾,了解对数的实际应用价值,体验其中蕴含的数学思想方法,并引导学生运用类比的方法,猜想对“对数”进一步研究的方向,诱发学生产生进行再探究欲望。
4.1.6 以史定教,凸现重构
要真正实现数学史有效地融入数学概念教学中,不仅需要教师注重挖掘数学知识点背后的历史,深入理解数学史的知识意义和方法意义,而且需要教师注重结合教学实际和学生的认知水平、数学基本活动经验,对数学史料进行有效地选择、加工,运用发生教学法,采用顺应式、重构式等有效的融入方式,将数学史中与所学的对数概念相关思想方法融入到新知识引入中,创设以数学史料为背景的问题链,引导学生进行自主探究,再现数学历史原貌,展示对数概念的发生、发展过程,让学生获得知识的过程中,体验其中蕴含的思想方法,促进学生去感悟和建构对数概念,理解对数概念所蕴含的本质特征,增强学习数学的信心,培养理性思考和执着的探求精神。 本节课应用了大量有关对数的数学史,由于其中涉及数列等一些学生并未学习或接触过的内容,在说法上作出了一些不影响史实的改动,并从历史发生原理出发,对有关对数知识历史发展过程中的关键步骤与环节,进而对知识的历史进行重构,使其适合学生认知和课堂教学,并设计一系列由易至难、环环相扣的问题。通过“重构” 历史上对数概念的发生、发展过程的方式,引导学生自己建构新概念,从而真正意义上理解对数概念的内涵和本质。
教师需要对所教主题的数学历史知识有深刻的理解,才能对知识的历史进行重构,以史为鉴,善于把“现成的知识”还原为“现实的问题”,创设富有数学历史背景的问题链,让学生在问题探究和解决中经历数学知识的发生、发展过程,并通过追寻大师的足迹、仰望大师的风采,汲取人类文明中的无穷智慧和坚韧不拨的探究精神。 如果仅一知半解、只见树木不见森林,知识的重构就难以达到“自然而然”的教学效果,数学史反而成了累赘。 其次,同一个数学家的历史故事,不同的讲述方式会产生不同的教学效果,教师会讲故事,也是一种教学实力。 再次,教师在运用数学史料时必须要把握尺度,或张或弛,或详或略,一切均以满足课堂教学的需求为准则,一方面,不能将数学课堂异化为“故事课”,另一方面,也不应只是简单用数学家的历史故事点缀一下课堂,匆匆带过,而应该要舍得花时间,给予学生倾听、领悟和思考的时空。在体验对数概念的生成过程中,引导学生思考,学会有效思考。进而能提出自己的观点和思路,逐步养成问题意识、探究意识和创新意识。





